Indian Sudoku Championship - December 2010 Monthly Test

Logic Masters India announces the December Sudoku Test 'XMas Special' which is a Classic Sudoku Relay. There were 12 Classic Sudokus. The relay indicates that there will be a set of digits that needs to be transferred from the 1st sudoku to the 2nd, from the 2nd to the 3rd and so on.
The author of the puzzles is the TTLC Team.

View Championship Page
Download Instruction Booklet
Download Puzzle Booklet
Password is 12XMas25
View Forum

Results

1. Jun Yan (China) - 1265
2. Ce Jin (China) - 1260
3. Jakub Ondrousek (Czech Republic) - 1250
4. Rishi Puri (India) - 1225
5. Don3232 (Taiwan) - 1100
6. Kota Morinishi (Japan) - 1075
7. Zafer Huseyin Ergan (Turkey) - 1075
8. RJH0723 (USA) - 1075
9. Greenhorn (Slovakia) - 1075
10. Florian Kirch (Germany) - 1075
11. Jakub Hrazdira (Czech Republic) - 1075

Best Indians

4. Rishi Puri - 1225
21. Sumit Bothra - 800
23. Gaurav Korde - 800
33. Rakesh Rai - 675
35. Akash Doulani - 575
44. Tejal Phatak - 575
46. Amit Sowani - 575

Complete Results

There were totally 146 participants.

I tested the puzzles. I completed the set in 106 minutes, so I would've probably completed 10 in 100 minutes. It was great fun organising the test offline in Mumbai. Also nice to see Sumit and Gaurav back! Looking forward to some more fun next year...

Solving Black And White: (Edge Connection)

One of the fundamental techniques of solving a Black And White puzzle which most beginners would not know is this edge rule. If two circles of the same colour are placed at an edge/corner, they must be connected along an edge.

Take a look at Puzzle No.37


You may be wondering how to start this puzzle!


Have a look at the marked circles. Both are black and placed at an edge/corner.


They have to be connected along an edge, which always gives two possibilities (two directions), marked in red and blue.


The connection along the red line is not possible due to the presence of the white circle. Hence the connection has to be made along the blue line. Pretty cool, isn't it? Now the puzzle is a piece of cake.


Using the 2x2 rule, you can place the three white circles. Now observe the circle at R3C2. It has to connect with other white circles and there is only one possible way, marked in red.


Using your brains and the rules, you should easily reach this situation.


And finally, with a small ending funda, complete it.

Now, looking back, did you realise how easy this puzzle becomes when you use this edge rule? I'm sure you will find Black And White puzzles very easy to solve now :-)

Other Solving Techniques

Solving Odd-Even Sudoku: (Section Solving)

The easiest method of solving an Odd-Even Sudoku is solving it in two parts. First solve the even numbers and then solve the odd numbers or vice-versa. The positions of the given odd numbers provides no clue for solving the even numbers and vice-versa, hence, it boils down to solving this sudoku in two sections.

Take a look at Puzzle No.266

Notice that every row/column/box contains four shaded cells, one for each even number.


Try solving the even numbers. Concentrate just on the even numbers and the shaded cells.


Using the basic sudoku rules, you should be able to solve it.


Now try solving the odd numbers. Concentrate just on the odd numbers and the unshaded cells.


Again using the basic sudoku rules, you should be able to solve it.


Thats it! Puzzle is solved! Use these two together and you should be able to crack any Odd-Even Sudoku without much trouble.

Other Solving Techniques

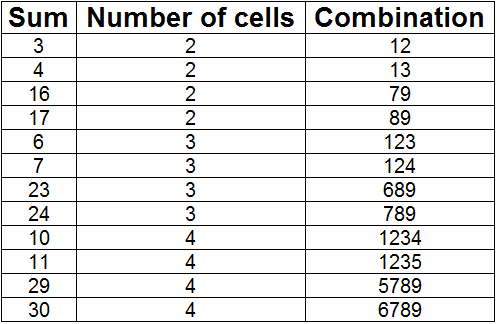
Solving Killer Sudoku: (Unique Combinations)

This is the basic concept you need to use for solving a Killer Sudoku. The list below gives the only possible combination of numbers for a given sum in different sizes of area (number of cells).

There are more such sets with higher area sizes, but these are the most commonly ones used.
The combination of numbers can occur in any order, but using these simple combinations can be very useful.

Other Solving Techniques

Forsmarts 8th Anniversary Online Contest

The 8th anniversary of the Forsmarts Online Contest was held on 18th December, 2010 at 16:00 - 18:00 GMT (21:30 - 23:30 IST).

View Championship Page

Download Instruction Booklet
Download Puzzle Booklet
Password is fs8WAtRFA

Results

1. Hideaki Jo (Japan) - 647
2. Nikola Zivanovic (Serbia) - 623
3. Jana Tylova (Czech Republic) - 593
4. Branko Ceranic (Serbia) - 538
5. Serkan Yurekli (Turkey) - 512
6. Kota Morinishi (Japan) - 500
7. Takuya Sugimoto (Japan) - 483
8. Shinichi Aoki (Japan) - 481
9. Taro Arimatsu (Japan) - 466
10. William Blatt (USA) - 455

Best Indians

24. Prasanna Seshadri (India) - 225
34. Anurag Sahay (India) - 20

Complete Results

There were totally 34 participants.

Very nice set of puzzles by Vladimir Portugalov in his typical style. Some of the puzzles were WPC 2010 type and I found Knight's Tale Sudoku the best with a beautiful logical solving path.

Puzzle No.337

Puzzle: Paint
Source: Indian Puzzle Championship 2010

PUZZLE NO.337: PAINT


SOLUTION:

Indian Puzzle Championship - December 2010 Monthly Test

Logic Masters India announces the December 2010 Monthly Test 'Puzzles And Chess'. It was held on 11th-12th December, 2010.
The author of the puzzles are Nikola Zivanovic.

View Webpage

Download Instruction Booklet
Download Puzzle Booklet
Password is chessMESS
View Forum

Results

1. Ulrich Voigt (Germany) - 123
2. Thomas Snyder (USA) - 111
3. Philipp Weiß (Germany) - 100
4. Hideaki Jo (Japan) - 95
5. Michael Ley (Germany) - 95
6. Psyho (Poland) - 93
7. Shinichi Aoki (Japan) - 87
8. Florian Kirch (Germany) - 84
9. Janka (Czech Republic) - 81
10. Branko Ceranic (Serbia) - 81

Best Indians

31. Rakesh Rai - 46
33. Rajesh Kumar - 43
44. Rohan Rao - 37
54. Prasanna Seshadri - 29
57. Rishi Puri - 27

Complete Results

There were totally 81 participants.

Beautiful puzzles. The usage of the chess pieces were very clinically done. The concept and implementation was brilliant.
Congrats to Ulrich, Thomas and Philipp for completing the set. Amazing performance by the Germans once again as they keep dominating the top 10.
And lastly, I wish I hadn't made those silly typos :-)

LMI tests are getting more exciting and more fun!

Puzzle No.336

Puzzle: Domino Hunt
Source: Indian Puzzle Championship 2010

PUZZLE NO.336: DOMINO HUNT (0~8)


SOLUTION:

Solving Classic Sudoku: 'X-Wing'

This is a very advanced sudoku solving technique. You need to have a great eye-sight to use this technique. If there is a number which can be placed only in two identical cells of different rows/columns, then that number cannot be placed in any other cell of the perpendicular columns/rows.

Take a look at this Classic Sudoku. Observe the 2nd and 6th rows.


In the 2nd row, '5' and '7' can only be placed in the cells marked in green. In the 6th row, '1' and '7' can only be placed in the cells marked in green.


The possible positions of '7' in the 2nd and 6th rows forms an x-wing and hence, '7' cannot be placed in any other cell of the perpendicular columns marked in red.


Using the '7' in R7C9, we find a unique position for '7' in the 7th box.

Other Solving Techniques

This post is supported by
Sudoku Online

Solving Classic Sudoku: 'Hidden Pairs/Hidden Triplets'

This is just an extension of 'Naked Pairs/Naked Triplets'. If there are two (three) cells of a row/column which can take any one number of a pair (triplet) of numbers, then no other number can be placed in those two (three) cells.

Take a look at this Classic Sudoku below. Observe the 2nd and 7th columns, alongwith the 3rd row.


The 2nd column has two empty cells for '7' and '8'. The 7th column has three empty cells for '7', '8' and '9'.


All the possible candidates of every cell of the 3rd row is given. Observe R3C2 and R3C7 in the 3rd row.


'7' and '8' can be placed either in R3C2 or R3C7 in the 3rd row. Hence these two cells cannot have any other number. Hence R3C7 cannot be '9'. Using other '9's, the '9' in the 3rd box can be placed uniquely.

Other Solving Techniques

Solving Classic Sudoku: 'Naked Pairs/Naked Triplets'

This is an advanced technique of solving a sudoku. It is hard to use this technique, but very useful! If there are two (three) cells of a row/column which can take any one number of a pair (triplet) of numbers, then that pair (triplet) of numbers cannot be placed in any other cell of that row/column.

Take a look at this Classic Sudoku below. Observe the 2nd, 4th and 8th columns, alongwith the 1st row.


The 2nd and 4th columns have two empty cells each for '4' and '6'. The 8th column has three empty cells for '4', '6' and '7'.


Observe R1C2, R1C4 and R1C8.


Since R1C2 and R1C4 are two cells which have to be the pair '4' and '6', they cannot be placed in any other cell of the 1st row. Hence, R1C8 cannot be '4', nor '6', and it has to be '7'.

Other Solving Techniques

Solving Classic Sudoku: 'Multiple Lines'

This is just an extended version of 'Double Pairs'. Instead of two identical cells, cells belonging to two rows/columns also follows the same result.

Take a look at Puzzle No.111. Observe the '7's.


The possible cells where '7' can be placed in the 6th and 9th boxes are marked in green.


Instead of two identical pairs of cells, it can be seen that all cells belong to the 7th and 8th column. Following the same rule as the earlier one, '7' cannot be placed in any other cell of the two columns. Hence the possible cells where '7' can be placed in the 3rd box is marked in green.


Let us just place the '4' in the 1st cell to understand this concept clearly. Using the '7's, check the possible cells where '7' can be placed in the 1st and 2nd boxes.


Using the 'Double Pairs' rule, R2C9 and R3C9 are eliminated and the unique cell left in the 3rd box has to be '7'.

Other Solving Techniques

Solving Classic Sudoku: 'Two Pairs'

This is a common technique used by top sudoku solvers. If you find a number occuring in the same to cells of two different adjacent boxes, then that number cannot occur in any other cell of the corresponding row/column of those two cells.

Take a look at Puzzle No.2. Try solving the centre box.


Using the earlier strategies, the centre box can be easily completed.


Observe the highlighted '4's and marked red cells which indicate cells where '4' cannot occur. Hence in the 2nd and 3rd boxes, the only possible cells where '4' can occur is marked in green.


Since '4' has to be placed in those two pairs of cells which are identical in adjacent boxes, '4' cannot be placed in any of the remaining cells of those two rows marked in red.


Observe the 1st box and using the '4' of the 1st column, there is a unique cell left where '4' can be placed.

Other Solving Techniques

Solving Classic Sudoku: 'Candidate Lines'

This technique is widely used to increase the speed of solving a sudoku. When a number has to be placed in one of the two (or more) cells of a box which are in a single row/column, the number cannot be placed in any other cell of that row/column.

Take a look at Puzzle No.75. Observe the '5' in the 1st box.


The possible positions of placing a '5' in the 2nd box is marked in green.


'5' has to be placed in either R1C4 or R2C4. Either way, '5' cannot be placed in any other cell of the 4th column, marked in red.


Using the '5' of the 6th column, there is only one unique position of placing a '5' in the 8th box, marked in green.

Other Solving Techniques

Solving Classic Sudoku: 'Single Candidate'

This is a very easy and straightforward method of finding a number. Select a cell (preferably with many given numbers in the corresponding row, column and box). If there is only one possible number that could be entered in the cell, it has to be that number.

Take a look at Puzzle No.104. We select R2C5 as it has many given numbers in the corresponding row, column and box.


The selected cell is marked in green.


All the numbers in the corresponding row, column and box are marked in red.


As 1, 3, 4, 5, 6, 7, 8 and 9 are present in the corresponding row/column/box of the cell, the only possible candidate for the cell is 2.

Other Solving Techniques