Solving Star Battle: (Solved Example 1)

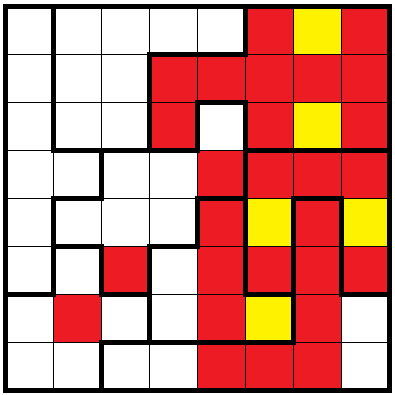
Take a look at Puzzle No.189

Each region is represented by an alphabet for convenience. Refer to this while reading through.

Using Region E, R5C7 can be eliminated. Using region F, R6C5, R6C6 and R8C5 can be eliminated. Using region H, R7C2 and R6C3 can be eliminated.

Observe regions G,F and H. If R6C8 is a star, the both stars of region G will be in the 8th row, which results in stars in R7C1 and R7C3 for region H leading to a contradiction in Region F. Hence, R6C8 is NOT a star.

Now the puzzle becomes very easy. Using Region E, R4C7 can be eliminated. One out of R4C6 and R5C6 has to be a star and hence R4C5 and R5C5 is eliminated.

Using Region F, we get a star in R7C6. All adjacent cells is eliminated.

Using Column 7, we get stars in R1C7 and R3C7, followed by stars in R5C6 and R5C8. After eliminating the remaining cells of row 5, you should be able to finish the puzzle.

Other Solving Techniques

Puzzle No.219

This is a Star Battle puzzle from the Indian Puzzle Championship - 2008.

PUZZLE NO.219: STAR BATTLE (2 Stars)


SOLUTION:

Puzzle No.189

This is a Star Battle puzzle that I created. It probably looks tough for beginners, but have a go at it, isn't as bad as it looks.

PUZZLE NO.189: STAR BATTLE (2 Stars)


SOLUTION:

Puzzle No.163

This is a Star Battle puzzle from the Belarusian Puzzle Championship - 2008.

PUZZLE NO.163: STAR BATTLE (2 Stars)


SOLUTION:

Puzzle No.160

This is a Star Battle puzzle.

PUZZLE NO.160: STAR BATTLE (2 Stars)


SOLUTION:

Rules of 'Star Battle'

Place the given number of stars in each row, column and thick-edged region of the grid. The stars do not touch each other, not even diagonally. Blackened cells cannot contain stars.

EXAMPLE: (1 STAR)

UNIQUE SOLUTION: