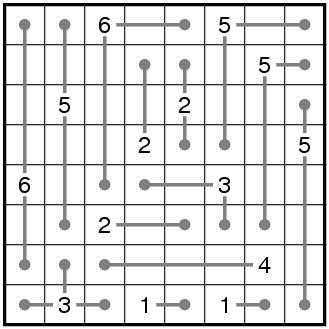
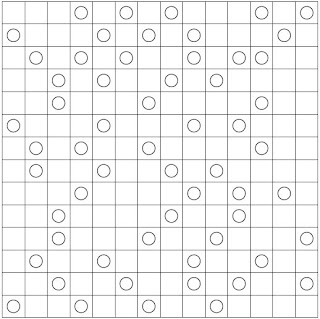
PUZZLE NO.48: CLASSIC SUDOKU

SOLUTION:

This blog deals with grid-based puzzles and the various types of logic and ideas used to solve them. It also contains notices, information and results about various puzzle and sudoku championships across the globe.